Some notes on computer screens, gamma, and CIE Rec. 709

The fact that computer screens have a non-linear response to RGB values is not a bug, as some people seem to think, it's a feature! It is meant to give a broader dynamic range, in correspondence to the way the human eye works.

One function that is meant to describe the transformation between RGB values and the monitor's luminance response is the gamma function, described by a power function: y = x**gamma. This is just an approximation, and it should not be expected that it is very accurate.

In fact, there are norms for how a computer screen should respond, one well known norm is the CIE Rec.709. In various software, one specifies a Gamma of 2.2. For example, PNG specifies a default gamma of 2.2. This value is taken from Rec.709, which reads:

PhotonCountToRGB(colour) {
	if (colour <= 0.018) {
		return 4.5 * colour;   /* toe slope */
	} else {
		return 1.099*pow(colour,0.45) - 0.099; /* scaled and transposed gamma
		                                        * function */
	}
}
RGBToPhotonCount(colour) {
	if (colour <= 0.081) {
		return colour / 4.5;
	} else {
		return pow((colour + 0.099) / 1.099, 1.0/0.45);
	}
}

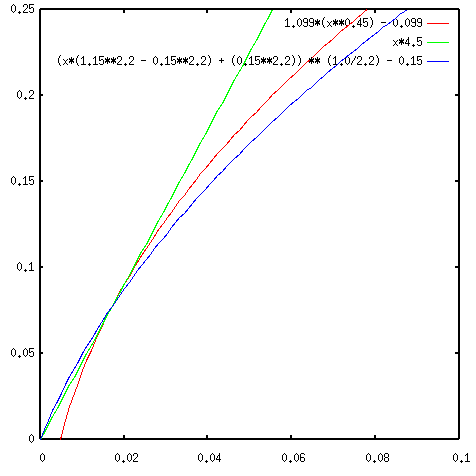
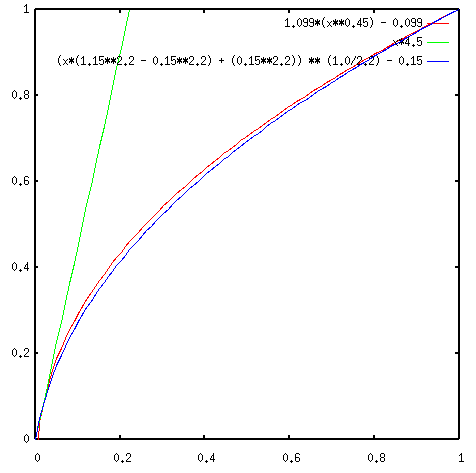
Basically it's a gamma function with a linear piece at the dark end (called the toe slope) to compensate for the sudden steepness at the dark end of the regular gamma function. So, 1/0.45 is 2.22. This is where the gamma of 2.2 comes from. However, the Rec.709 is also scaled and transposed. When one plots the Rec.709 function (forgetting about the toe slope for a moment, plotted in red), it is much closer to a gamma of 1.8 (blue) than 2.2 (green). See the plot below.

Concluding, we may say that a gamma of 2.2 is NOT the most accurate approximation of the Rec.709 function.

A simple and general alternative for the `toe slope'

Rec.709 also indicates that a plain gamma function is not very good at the very darkest end of the brightness range. It suggests a very broad range of shades from near-black to black, while in reality the computer screen's actual response may even mean a flatter curve there, rather than a steeper one. I've been trying to make a generalised alternative to the Rec.709's strategy of piecing together two functions. A very simple alternative to get rid of the too-steep dark end, is to transpose the function to the left, and then scale it so it has domain [0:1] and range [0:1] (function drawn in blue, transposed by 0.15). It closely fits the Rec.709 function. See the plots below. The right plot shows a detail of the left one. The reason for the toe slope seems to be apparent in this plot as well: the gamma function is very steep here. The toe slope (green) ends when it intersects the 709's transposed/scaled gamma (red).